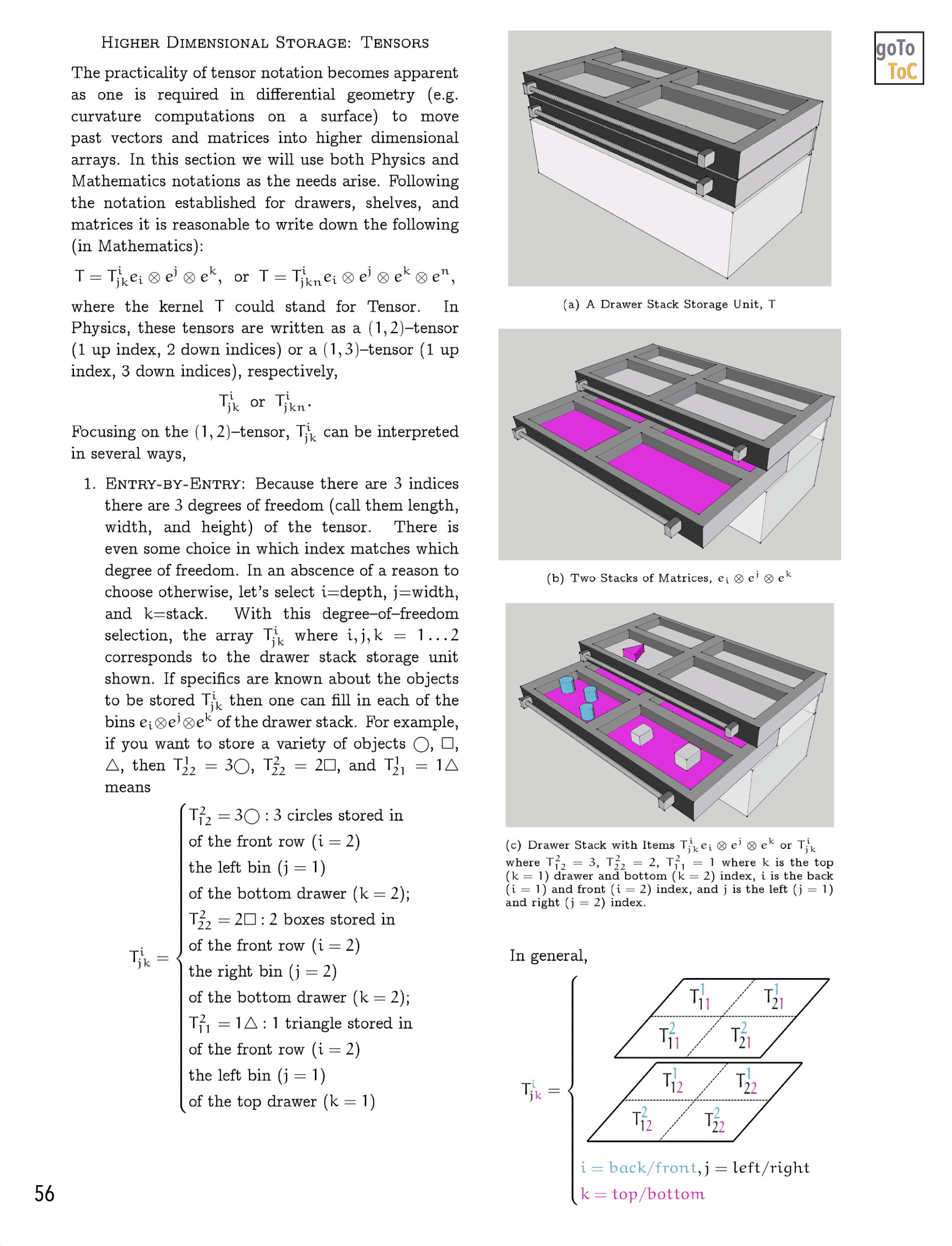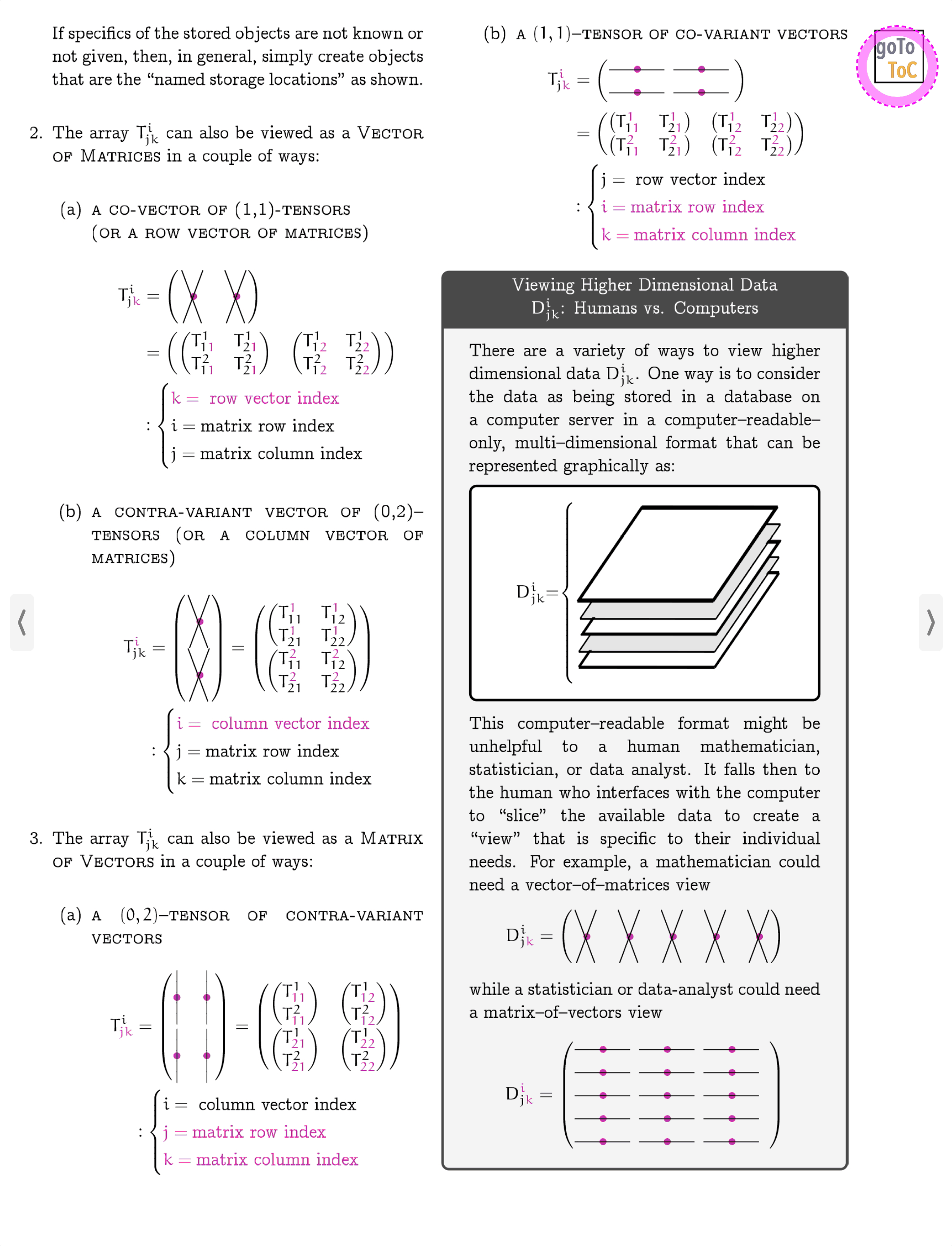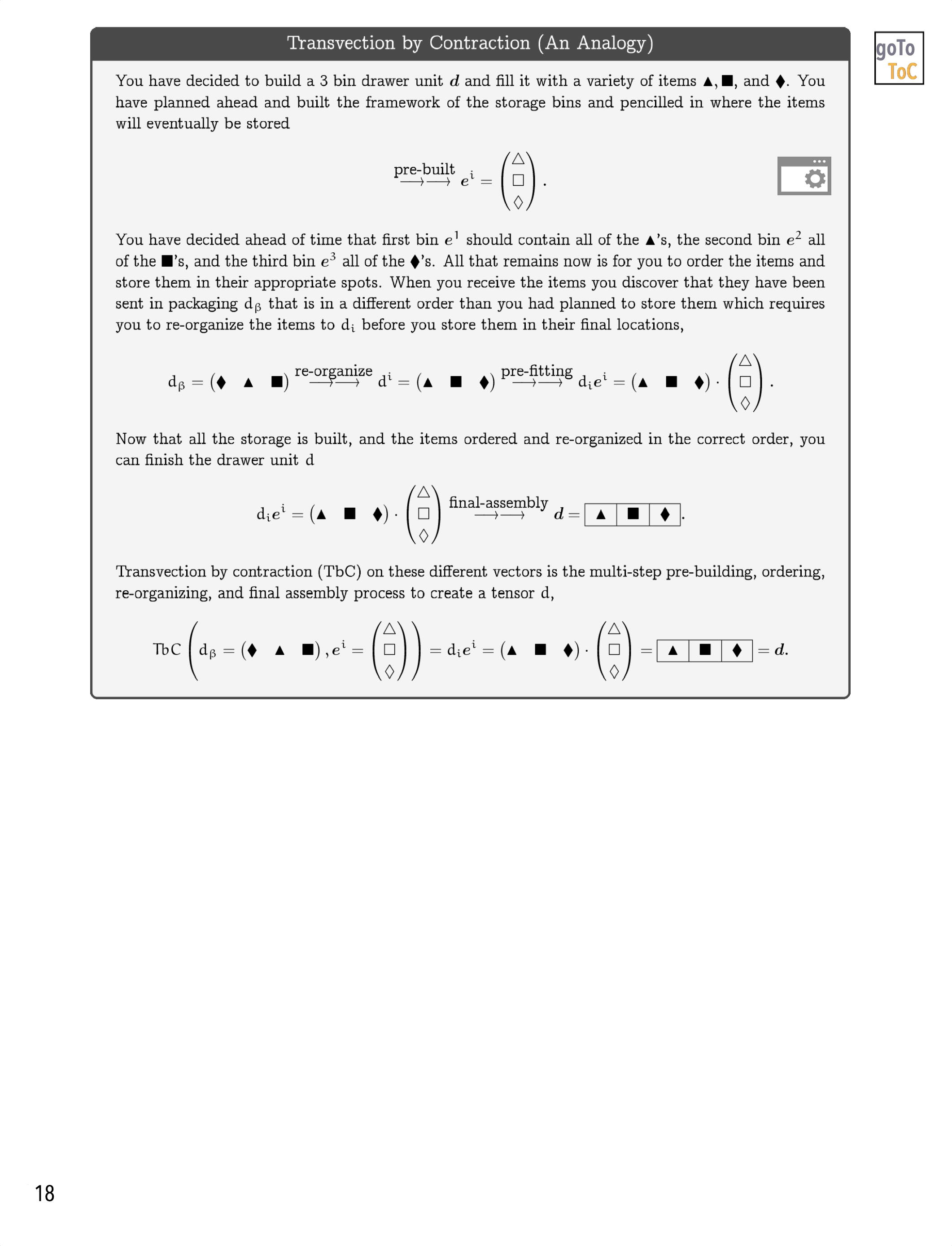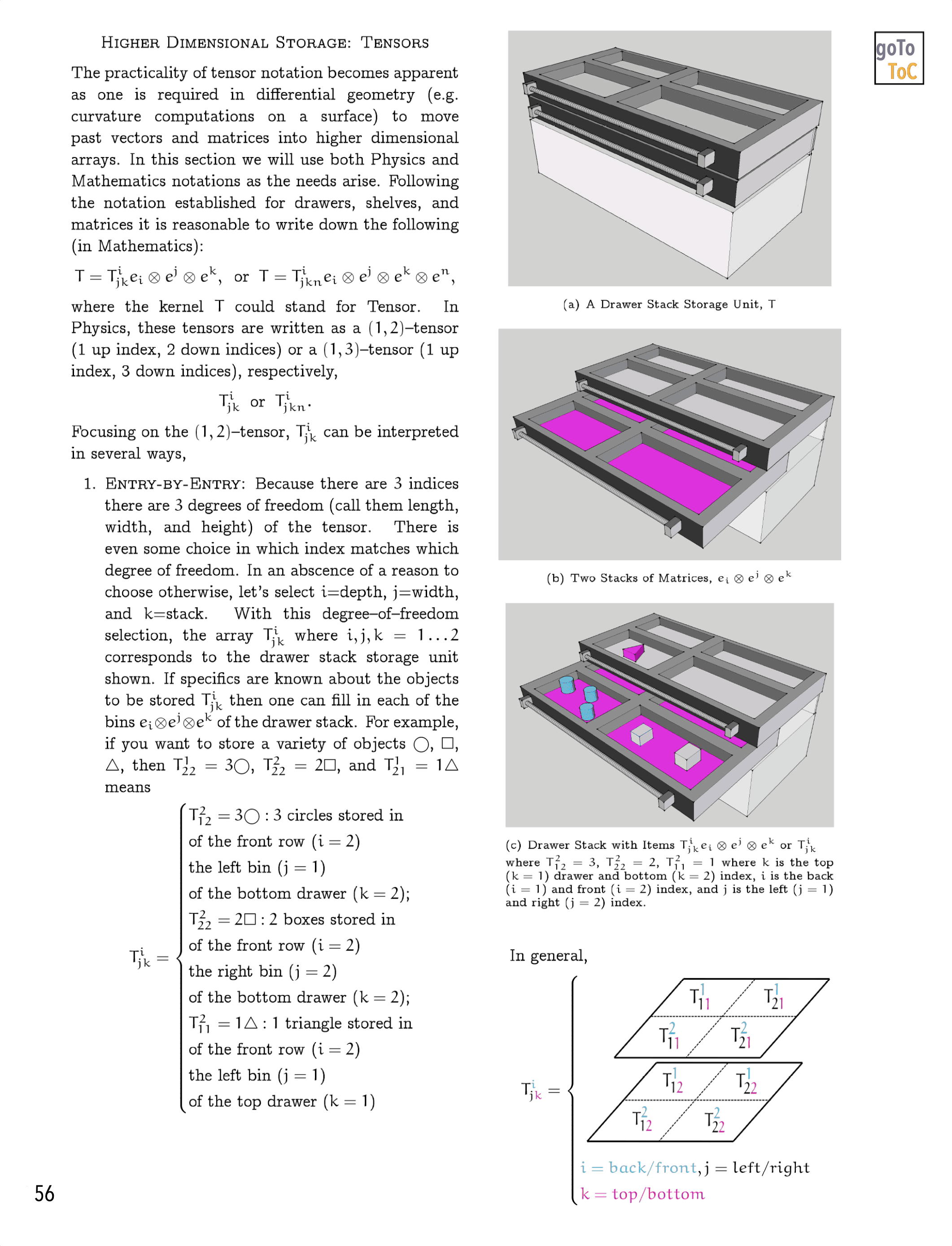
On Tensors…
…is now available as an interactive, animated eBook on Apple Books. In this post, similar to that given on our LinkedIn page (Featured Section) , we give a short summary of this book. From Linear Algebra to Surface Curvature: The Mathematics of a Curvature Story. Starting from introductory Linear Algebra (matrices, vectors, and multiplications thereof) we develop the Kernel-Index or Tensor Notation as written about by J.A. Schouten in the book Ricci-Calculus. Concepts from Linear Algebra are motivated by way of Colors and Tensors are motivated as a means of Storage. The Linear Algebra and Tensor machinery converge with a treatment of the computation of Surface Curvature from both an intrinsic and extrinsic point of view. We conclude with both graphical and computational illustrations of Gauss’ Theorema Egregium.

Last Updated: Wednesday, January 03, 2024 - 12:31:06.
So Many Questions
Have you ever tried to learn about the Tensors of Differential Geometry and run into the wall of Index Notation? Have you ever thought about Linear Algebra in terms of Color? Did you know that Linear Algebra and Tensors are related? Did you ever see a geometry book that dealt with Curvature and wished for more pictures? Have you ever seen all these topics addressed in One Interactive, Graphically Intensive, Yet Mathematically Complete Book?
It’s Finally Here! Read this book and change your life.

Figure 1: Here the full book link, https://books.apple.com/us/book/id6463653068
A Books Series Finally Completed
The book OnTensors completes a series of books which offer a graphical tour through of some of the foundational ideas of Differential Geometry.

Figure 2: Here is the page containing all the book links, https://unconcise.com/blog

Figure 3: Here is the Table of Contents for the eBook On Tensors

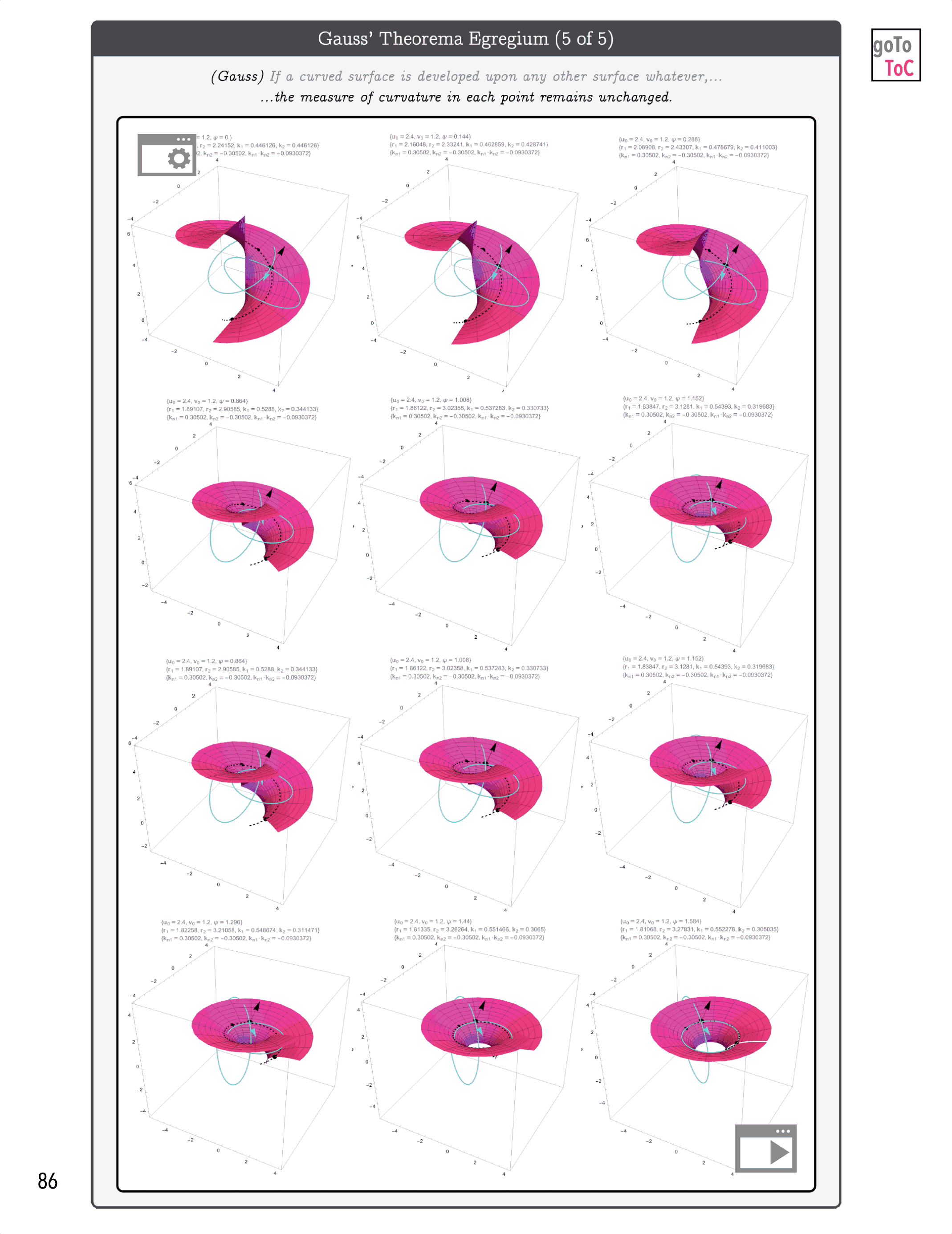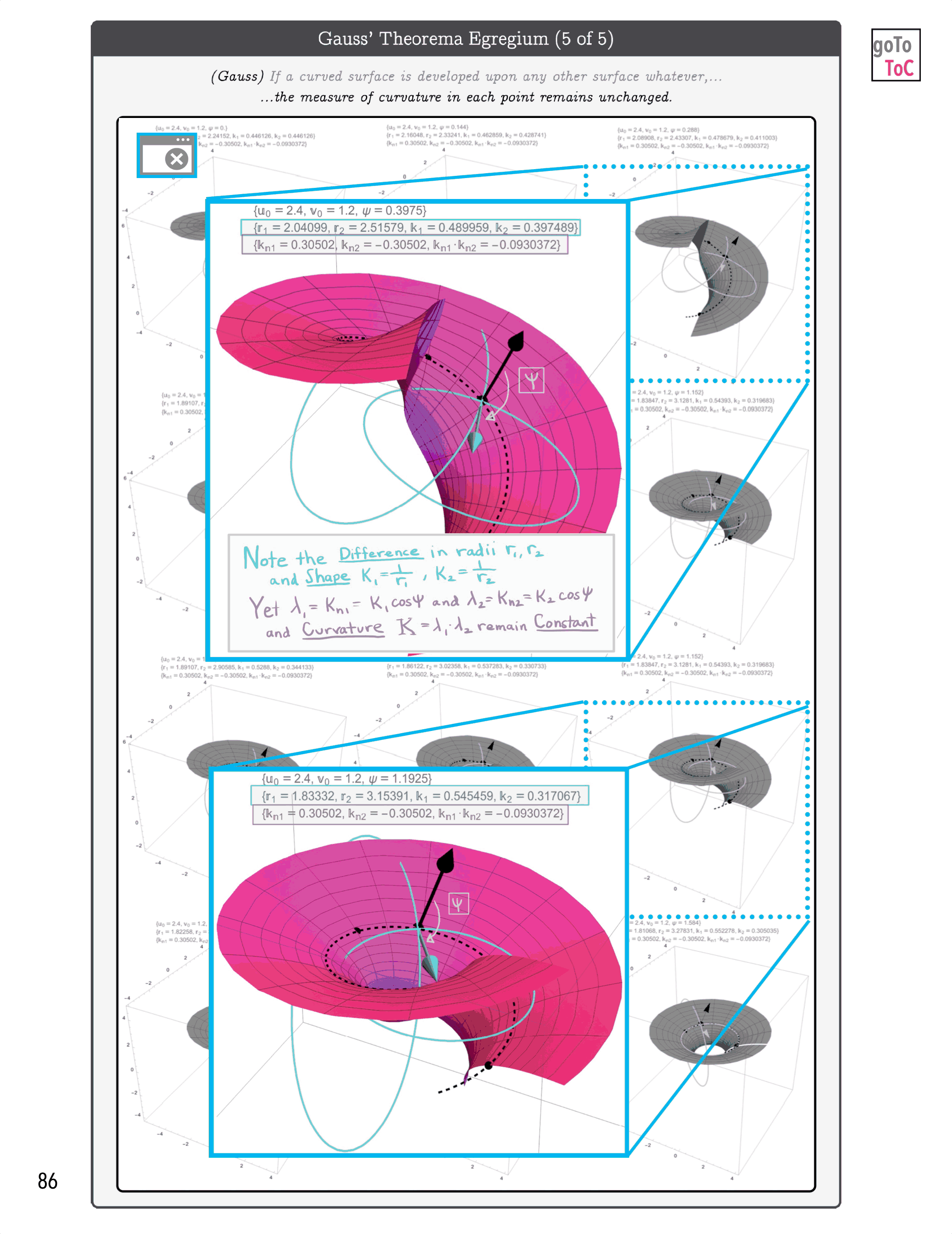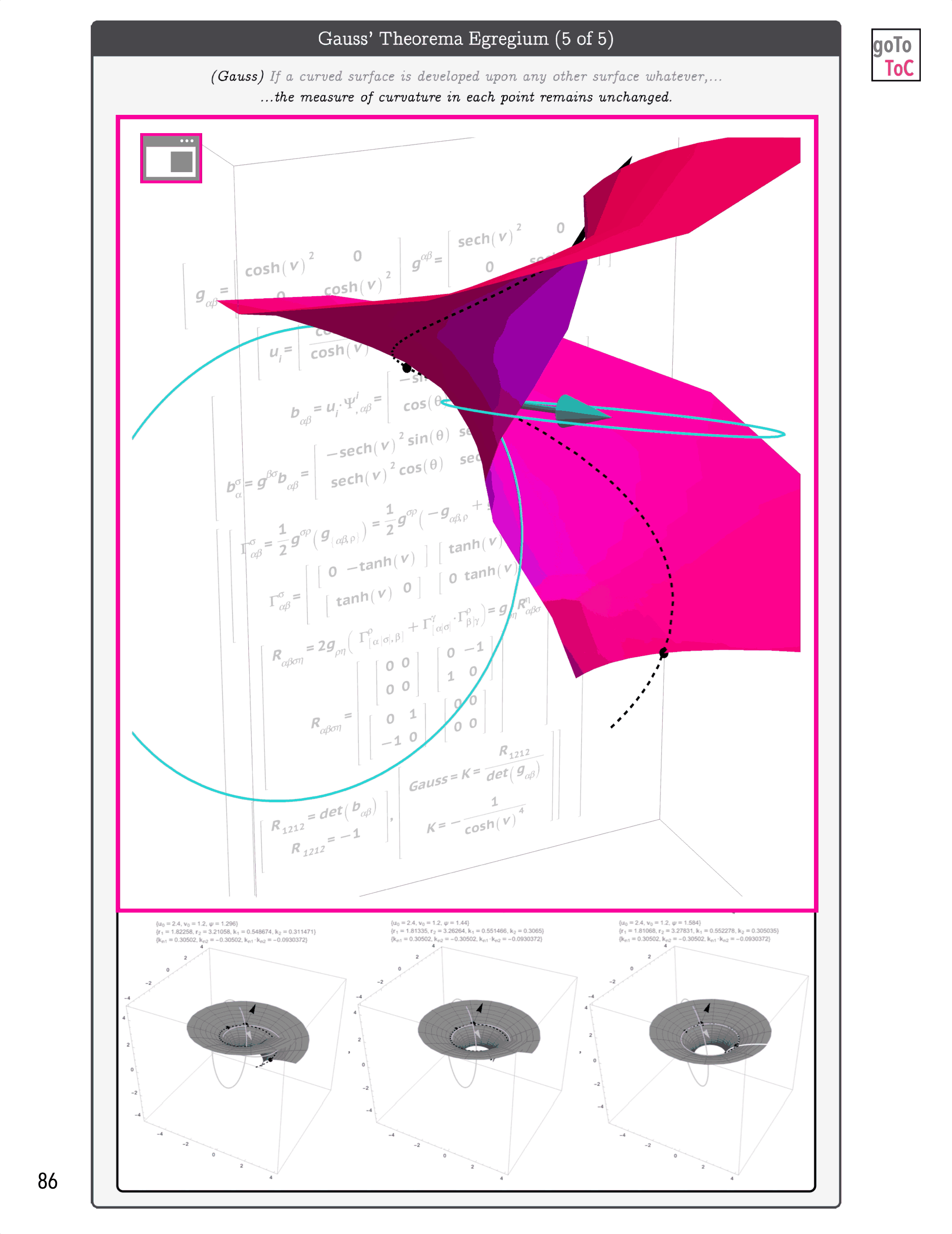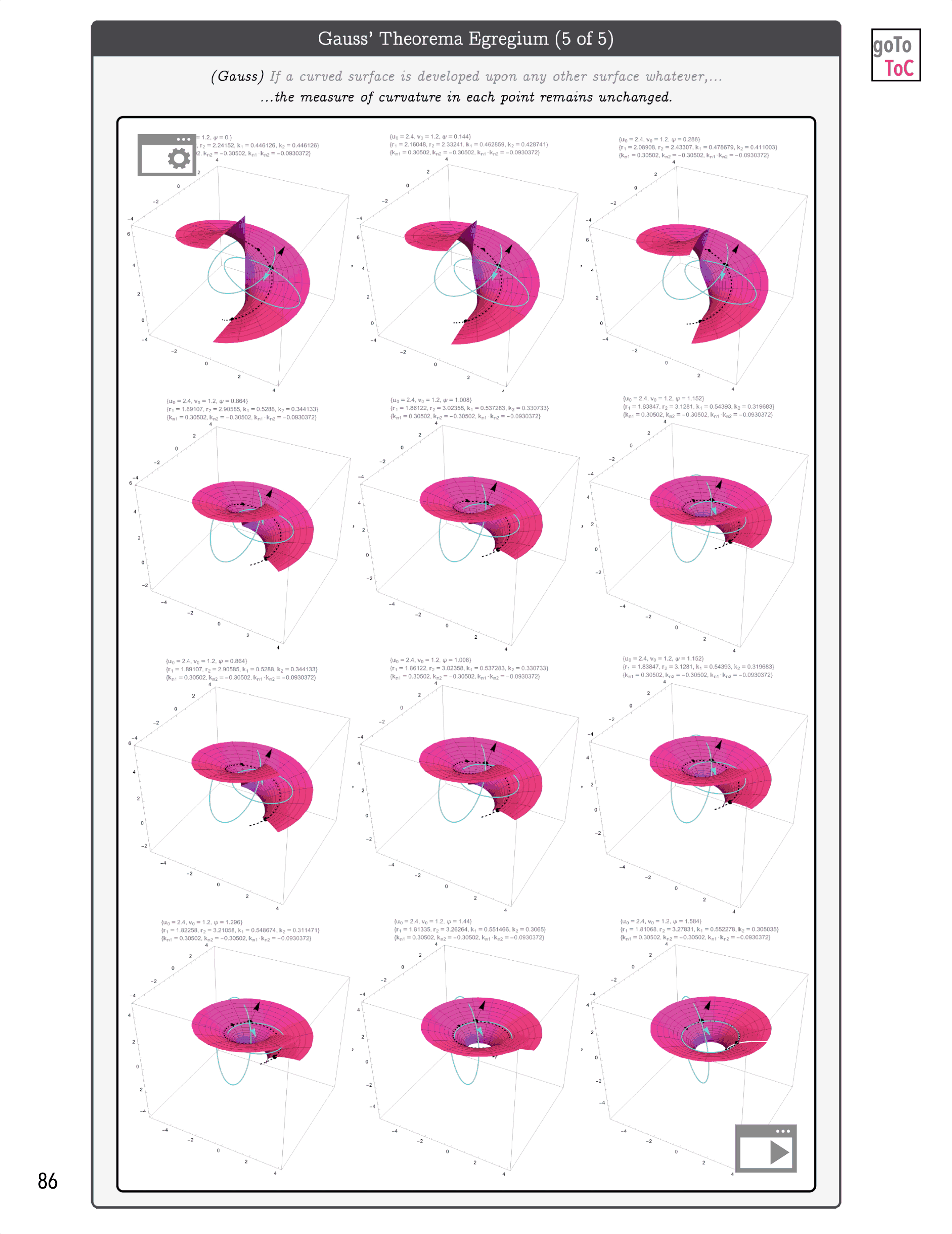
Figure 4: An animated peak inside of the eBook On Tensors
Follow us in this this book as we:
Introduce concepts…
…from Linear Algebra with always an eye towards Tensors.

Figure 5: Our Goal is to gradually build an understanding of the mathematical machinery of the Kernel-Index Method as written about by J.A. Schouten in Ricci-Calculus
Further develop…
…ideas in Linear Algebra and Tensors within the context of Color.
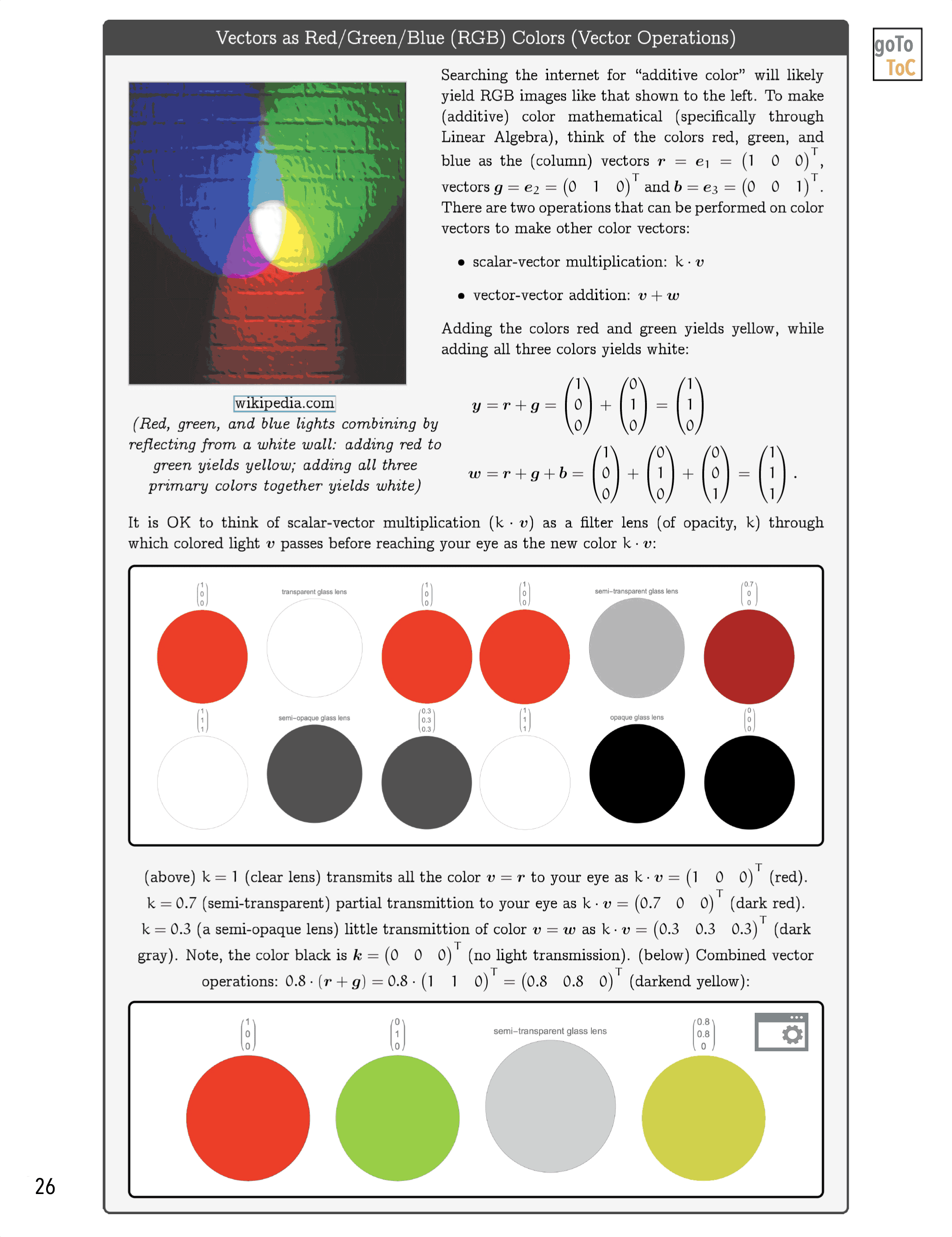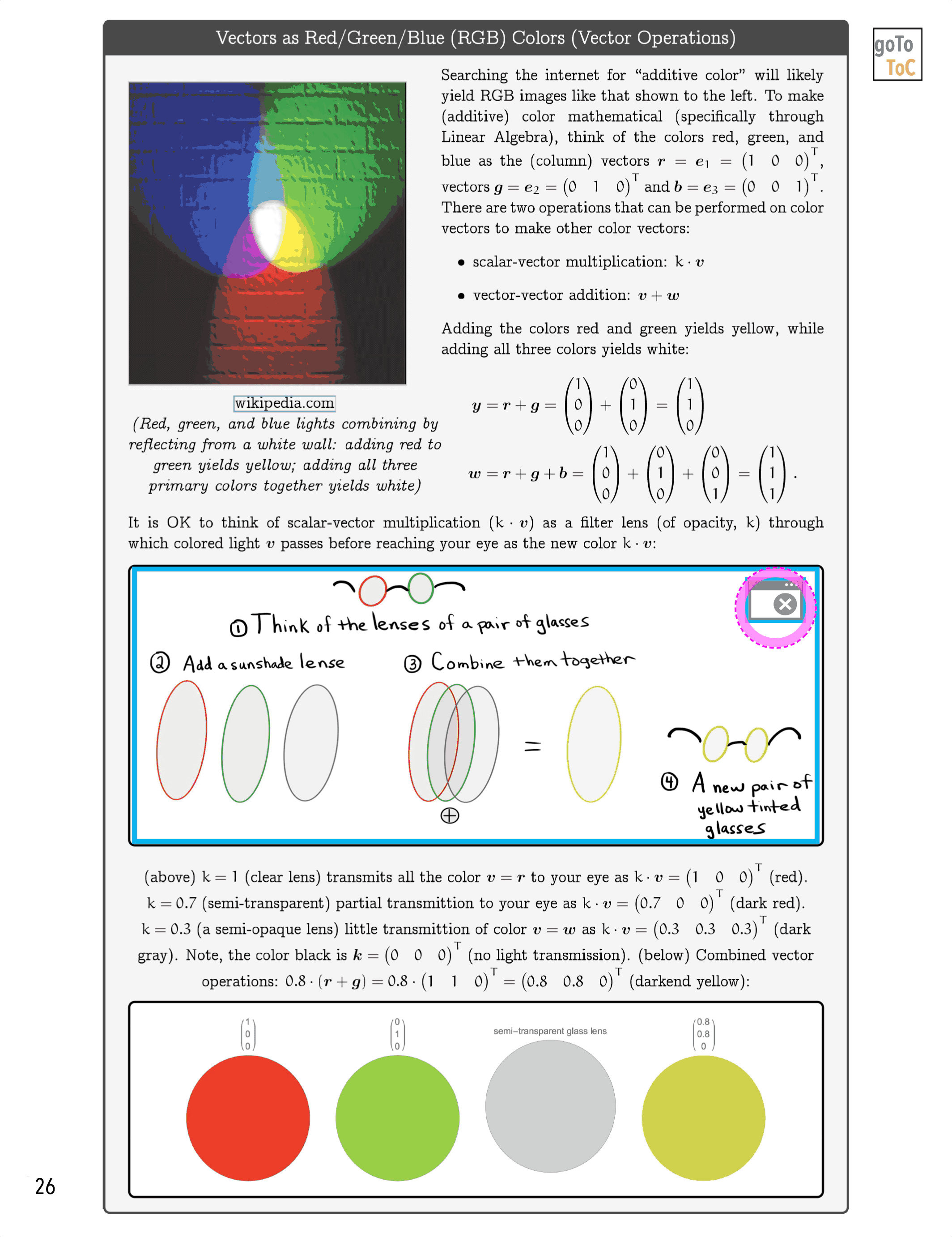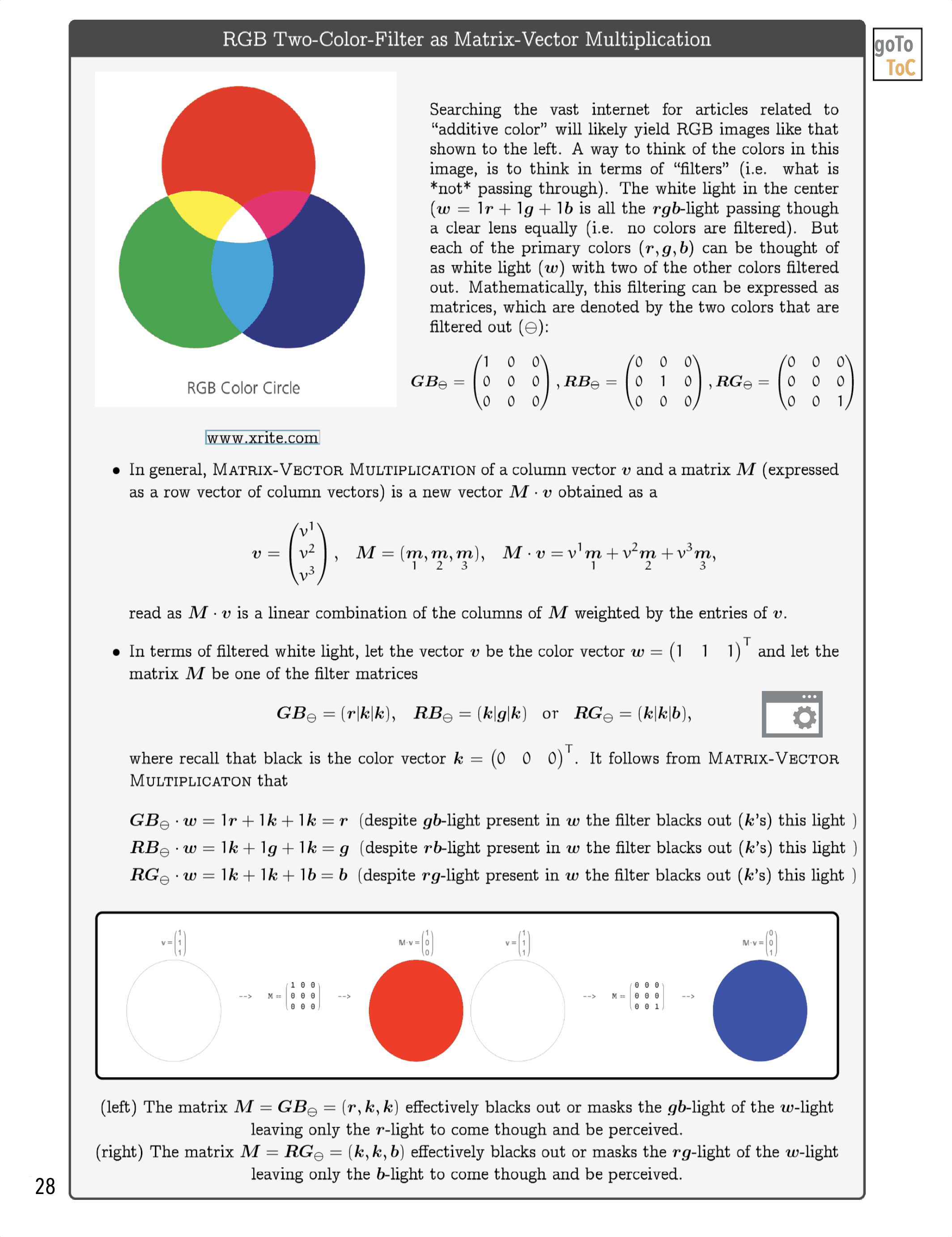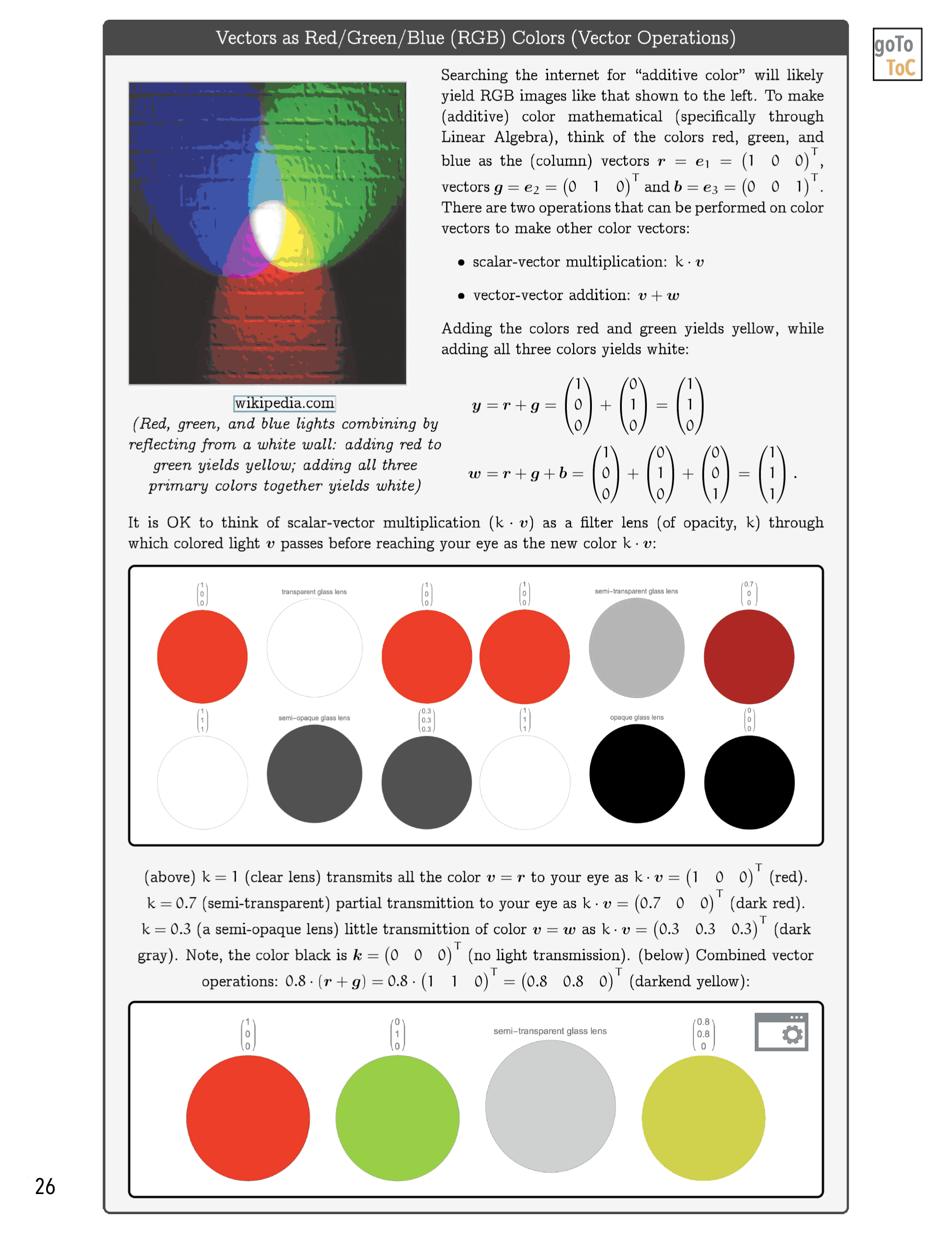
Figure 6: We attempt to illustrate mathematical ideas from Linear Algebra in ways that might not be commonly utilized
Extend…
…the graphical treatments of differential geometry in our previous books to include more mathematical detail.

Figure 7: On Tensors Extends the Graphical Ideas Introduced in Previous Books to Include More Mathematical Detail
Find video summaries of this series of books on https://unconcise.com/blog
Not into the geometric subject matter of these books?
No problem. Try this post An UnConcise/math Vision for eBooks from my blog www.unconcisemath.com which discusses my general thoughts on the promises of an unConcise/math style eBook.
Coming Up Next
With a grounding in Tensors and Tensor Computations as discussed in the book On Tensors we begin to transition into differential geometric computations for (the many forms of) Derivatives. These results will involve an interesting amalgamation of tools and techniques. We will be happy to show how the output of computations from software like Maple (by MapleSoft) can be used as the input to software like Mathematica (by Wolfram Research) which can be used to illustrate geometric concepts like Parallel Transport, etc.

Figure 10: Output from Tensor Computations in Maple (MapleSoft) Become the Input to Mathematica (Wolfram Research) for Creating Geometric Plots