Convert Maple Output to Mathematica Input

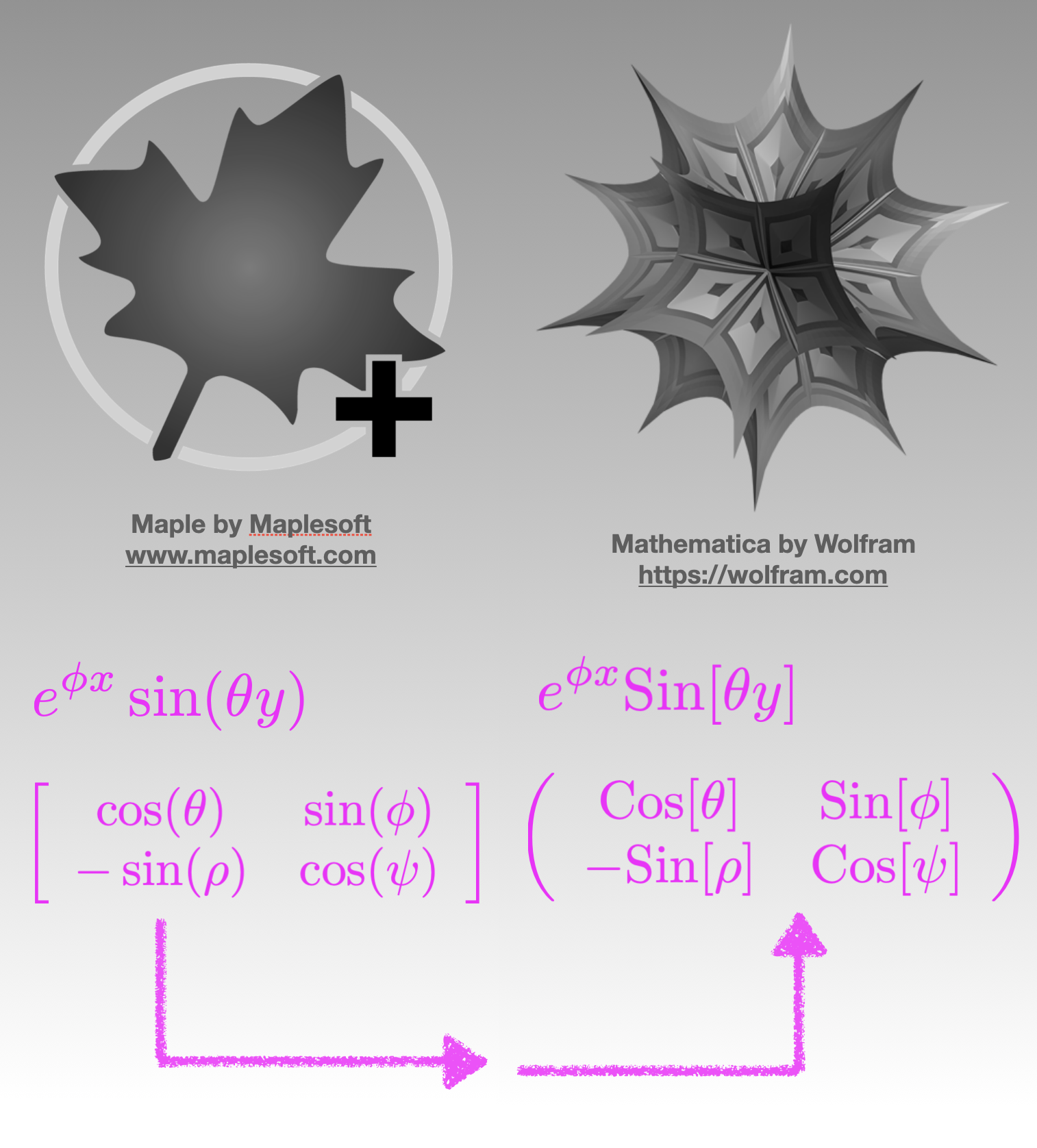
If you are like me, then you are familiar with and use both Maple and Mathematica. You also know that these two mathematical software products use different syntax. These syntactical differences can make passing the output from one product to the other an annoying challenge.

In my workflow, I greatly appreciate the computational abilities of Maple in the realm of Tensors, while I also love the graphical and general computational capabilities of Mathematica. To help bridge these two products, I have found a way (through MathML) to convert Maple output to Mathematica input.

For example, in Maple you would write an expression as \(\sin(\theta)\). However, in Mathematica, you would write this same expression as \(\mathrm{Sin}[\theta]\). While it is not difficult to convert parens () to square brackets [] or to change lower case \(\sin\) to upper case \(\mathrm{Sin}\) in a single expression and on a case-by-case basis, this process is annoyingly ineffective and a complete wast of time as the number of expressions grows (> 2).

In this post, we demonstrate a programmatic method to convert Maple output to Mathematica input.

Last Updated: Wednesday, January 03, 2024 - 12:31:59.

An Infographic Solution…

… with details to follow in the post below.

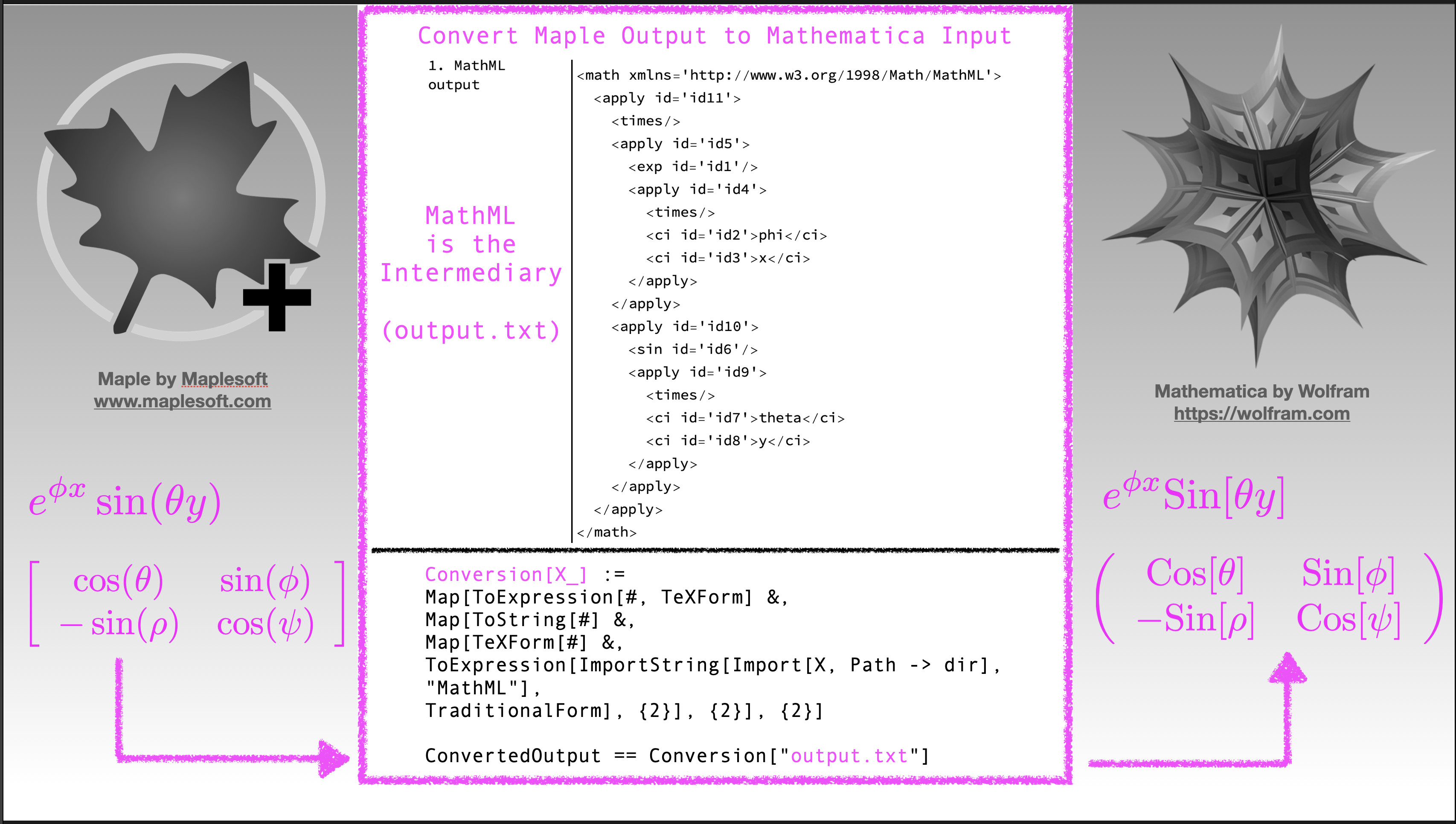
Figure 1: Convert Maple Output to Mathematica Input

Details: Define a Maple Expression…

…and write the MathML content to a text file.

Figure 2: Define a Maple Expression and Write the MathML Content to a Text File

output := exp(phi*x)*sin(theta*y);

writeto("output.txt");
XMLTools[Print](MathML['ExportContent'](eval(output)));
writeto(terminal);

# the MathML output text file will be written  
# in the same directory as the Maple file

Details: Using a Conversion in Mathematica…

…if the Maple output is an expression.

Figure 3: A Conversion of Maple Output (an expression) to Mathematica Input (an expression)

(* set the path dir to be the location *)
(* where the MathML text file resides *)

dir = "/Users/name-of-your-computer/Documents";

  ExpressionConversion[X_] := 
  ToExpression[
   ToString[
    TeXForm[ToExpression[
      ImportString[Import[X, Path -> dir], "MathML"], 
      TraditionalForm]]]
   , TeXForm];
   
ConvertedOutput == ExpressionConversion["output.txt"]

Motivation: A Proof-of-Concept Expression Conversion…

…and how it works.

Unfortunately this conversion works only for expressions (and not, for example, for vectors or matrices). Don’t worry, we will show a general conversion method soon that works for expressions, vectors, and matrices!

The Conversion of Maple Expressions Output to Mathematica Input Works in Three Steps 1. Import the Maple Output as a MathML Text File 2. Convert parens () to square brackets [] and lower case to upper case function names 3. Replace Greek Words with Greek Symbols

Figure 4: The Conversion of Maple Expressions Output to Mathematica Input Works in Three Steps 1. Import the Maple Output as a MathML Text File 2. Convert parens () to square brackets [] and lower case to upper case function names 3. Replace Greek Words with Greek Symbols

Problem: If You Use Expression Conversion on Matrices…

…then you will get undesirable behavior.

Figure 5: If the Maple Output is a Matrix and the Expression Conversion is Used in Mathematica, Then an Undesirable Conversion Will Occur.

Conclusion: Here is a General Maple to Mathematica Conversion…

…that works for Maple output as an expression, vector, or matrix.

Figure 6: A General Conversion of Maple Output (expression, vector, or matrix) to Mathematica Input

# output := exp(phi*x)*sin(theta*y)
# output := Matrix(1, 2, [cos(theta), sin(phi)]);
output := Matrix(2, 2, [[cos(theta), sin(phi)], [-sin(rho), cos(psi)]]);

writeto("output.txt");
XMLTools[Print](MathML['ExportContent'](eval(output)));
writeto(terminal);

(* if the Maple output is an expression, vector, or a matrix *)
(* then use this more general conversion in Mathematica *)

dir = "/Users/name-of-your-computer/Documents";

Conversion[X_] := 
 Map[ToExpression[#, TeXForm] &, 
  Map[ToString[#] &, 
   Map[TeXForm[#] &, 
    ToExpression[ImportString[Import[X, Path -> dir], "MathML"], 
     TraditionalForm], {2}], {2}], {2}]

ConvertedOutput == Conversion["output.txt"]

Extension: Why Do We Care?

Recently, I have completed an eBook on Apple Books called On Tensors, which itself completes a series of books which offers a graphical tour through of some of the foundational ideas of Differential Geometry. In all of these books we used a mixture of Maple and Mathematica to complete the computationally-generated, mathematically-correct, and often-animated artwork. Behind the scenes we often needed to use the Maple Output to Mathematica Input conversion code as part of artwork-creation-process.

Figure 7: Here is the page containing all the book links, https://unconcise.com/blog

Figure 8: Here is the Table of Contents for the eBook On Tensors

Coming Soon: Conversion in Action Behind the Scenes

With a grounding in Tensors and Tensor Computations as discussed in the book On Tensors, future posts and eBooks will transition into differential geometric computations for (the many forms of) Derivatives. These results will involve an interesting amalgamation of tools and techniques. As we have seen in this post, the output of computations from software like Maple (by MapleSoft) can be used as the input to software like Mathematica (by Wolfram) which can then be used to illustrate geometric concepts like e.g. Parallel Transport.

Output from Tensor Computations in Maple (MapleSoft, on left) Become the Input to Mathematica (Wolfram Research, on right) for Creating Geometric Plots

Figure 9: Output from Tensor Computations in Maple (MapleSoft, on left) Become the Input to Mathematica (Wolfram Research, on right) for Creating Geometric Plots